resume

MTA EDA & Machine Learning

Exploratory Data Analysis & Machine Learning on one year of NYC subway data

Created with:

Python

Year

2023

View Project

MTA EDA & Machine Learning

Exploratory Data Analysis & Machine Learning on one year of NYC subway data

Created with:

Python

Year

2023

View Project

Render is loading. Please wait or press 'View Project' at the top of the page

Understanding the dataset

This data set is provided by the Metropolitan Transportation Authority via the NYC Open Data platform. The ridership metrics provided may differ slightly, but are within 1% of ridership figures provided at public MTA board meetings. Data is released weekly. The latest version of the dataset can be found here.

Potential Goals of Analysis

What is the best time to schedule maintenance?
Which factors are most important to ridership (time of day, day of week, etc.)?
Which part of the city has the most riders? Which Borough?
Which station sees the most riders?
Does Subway usage have seasonal trends?
Is there potential to build a model to predict ridership?

Overall by answering these questions and gaining a further understanding of ridership, it should highlight that the MTA could use data to improve crowd management, service performance and maintenance scheduling.

The most necessary columns for our analysis are the following:

transit_timestamp (to identify the time of day)
station_complex (to identify the station)
ridership (to identify the number of people entering the station at a given time)
latitude / longitude / Georeference (to identify the location of the station)

1. Importing the required libraries

import pandas as pd # for data manipulation and analysis
import numpy as np

import seaborn as sns # for data visualization
import matplotlib.pyplot as plt
import plotly.express as px

import dash # for building interactive visualizations
from dash import dcc, html, Input, Output

import geopandas as gpd # for geographic data manipulation
from shapely.geometry import Point, Polygon

from sklearn.model_selection import train_test_split # for machine learning
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score

2. Preparing the data

Read CSV to Dataframe

# read csv file to pd dataframe
df = pd.read_csv('MTA_Subway_Hourly_Ridership__Beginning_February_2022.csv')

Preparing the data for datetime format

# change transit_timestamp to datetime object
df['transit_timestamp'] = pd.to_datetime(df['transit_timestamp'])

Make a copy before slicing the dataset

original_df = df.copy()

Get data for one year

Since the data begins on February 1st 2022 we will use the data from Feb. 2022 → Feb. 2023. This will allow us to have an even distribution and outliers such as holiday will only occur once in the data.

# Filter data for the specified time range
start_date = pd.Timestamp('2022-02-01')
end_date = pd.Timestamp('2023-02-01')
df = df[(df.transit_timestamp >= start_date) & (df.transit_timestamp < end_date)]

# check the earliest and latest time of the data
print(df['transit_timestamp'].min())
print(df['transit_timestamp'].max())

Output:

2022-02-01 00:00:00 2023-01-31 23:00:00

Clean the names of the stations by removing the route numbers

# remove the () and everything in between the () from each station_complex row in the df
df['station_complex'] = df['station_complex'].str.replace(r'\(.*\)', '', regex=True)

Preparing the data for geovisualization

# make geodataframe out of df
gdf = gpd.GeoDataFrame(df, geometry=gpd.points_from_xy(df['longitude'], df['latitude']))

geo_stations_df = gdf.groupby(['station_complex_id', 'station_complex', 'borough', 'latitude','longitude', 'geometry'])['ridership'].sum().reset_index()

3. Exploratory Data Analysis

How many subway stations in our dataset?

# print the number of unique station complex ids
print(df['station_complex_id'].nunique())

423

Create a new dataframe grouped by station and ridership

by_station_df = df.groupby(['station_complex_id', 'station_complex', 'borough', 'latitude', 'longitude'])['ridership'].sum().reset_index() by_station_df.shape

Riders by borough

## get the total ridership by borough
boroughs = df.groupby('borough')['ridership'].sum()
boroughs

borough
BK 237932586
BX 81994749
M 560176396
Q 156471936

Visualizing the amount of ridership by borough

fig = px.treemap(boroughs, path=[boroughs.index], values=boroughs.values, title='Subway Ridership by Borough')
fig.show()

We can see that Manhattan has the most ridership, followed by Brooklyn, Queens and the Bronx.

Visualizing the number of stations by borough

station_count = by_station_df['borough'].value_counts()
borough_names = ['Brooklyn', 'Manhattan', 'Queens', 'Bronx']

fig = px.bar(x = borough_names, y = station_count.values, 
       color = station_count.index, text = station_count.values, 
       title = 'Number of Stations by Borough')

fig.update_layout( xaxis_title = "Boroughs", yaxis_title = "Subway Stations")
fig.show()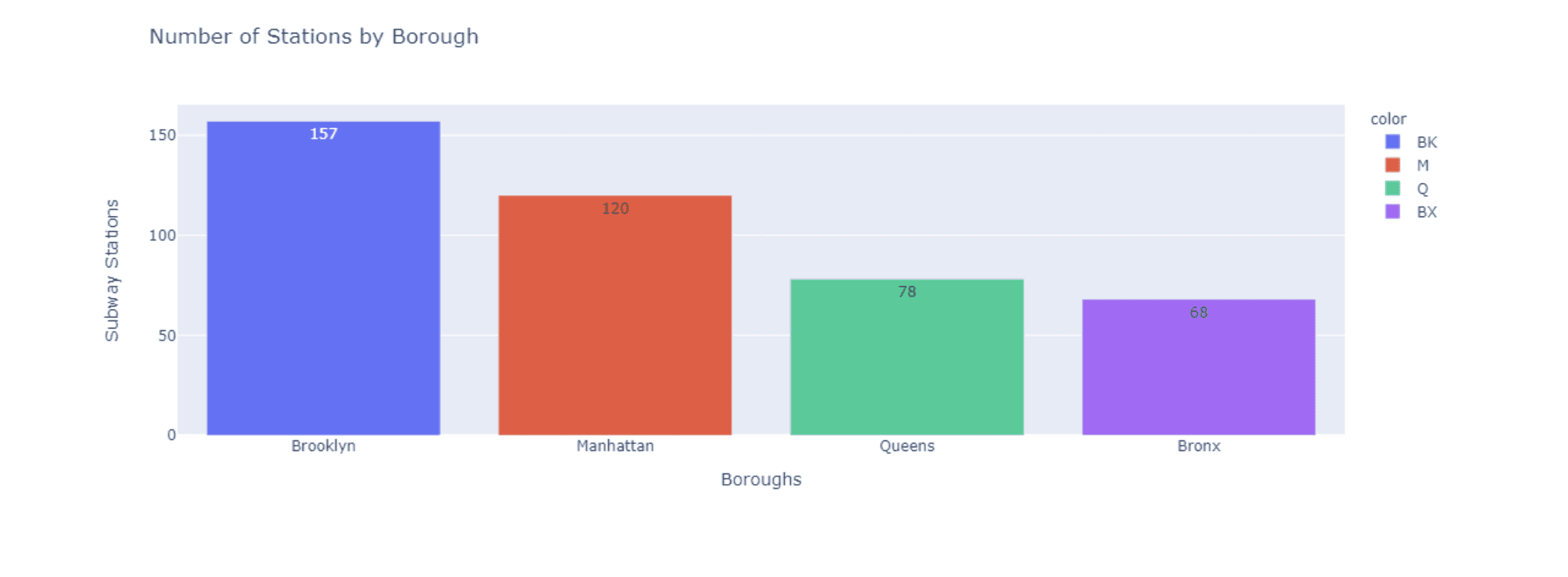

We can see that Manhattan actually has less stations despite having the most ridership.

Using a strip plot it allows us to see that each borough has a high concentration of stations with a low number of ridership. Each borough has a few stations with a much higher ridership than the rest, we can also see just how vast the difference is between the Times Sq-42 St station and the rest of the stations.

# make a copy of by_station_df and divide the ridership by 1 Million to normalize the data to millions
by_station_df_normalize = by_station_df.copy()
by_station_df_normalize['ridership'] = by_station_df_normalize['ridership']/1000000

sns.stripplot(x=by_station_df_normalize['ridership'], y=by_station_df_normalize['borough'], hue=by_station_df_normalize['borough'])
plt.yticks([0, 1, 2, 3], ['Manhattan', 'Brooklyn', 'Queens', 'Bronx']) 
plt.xlabel('Total Ridership in Millions')
plt.ylabel('Borough')
plt.annotate('Times Sq-42 St', xy=(0.76, 0.915), xycoords='axes fraction')
plt.title('Ridership by Borough')
plt.show()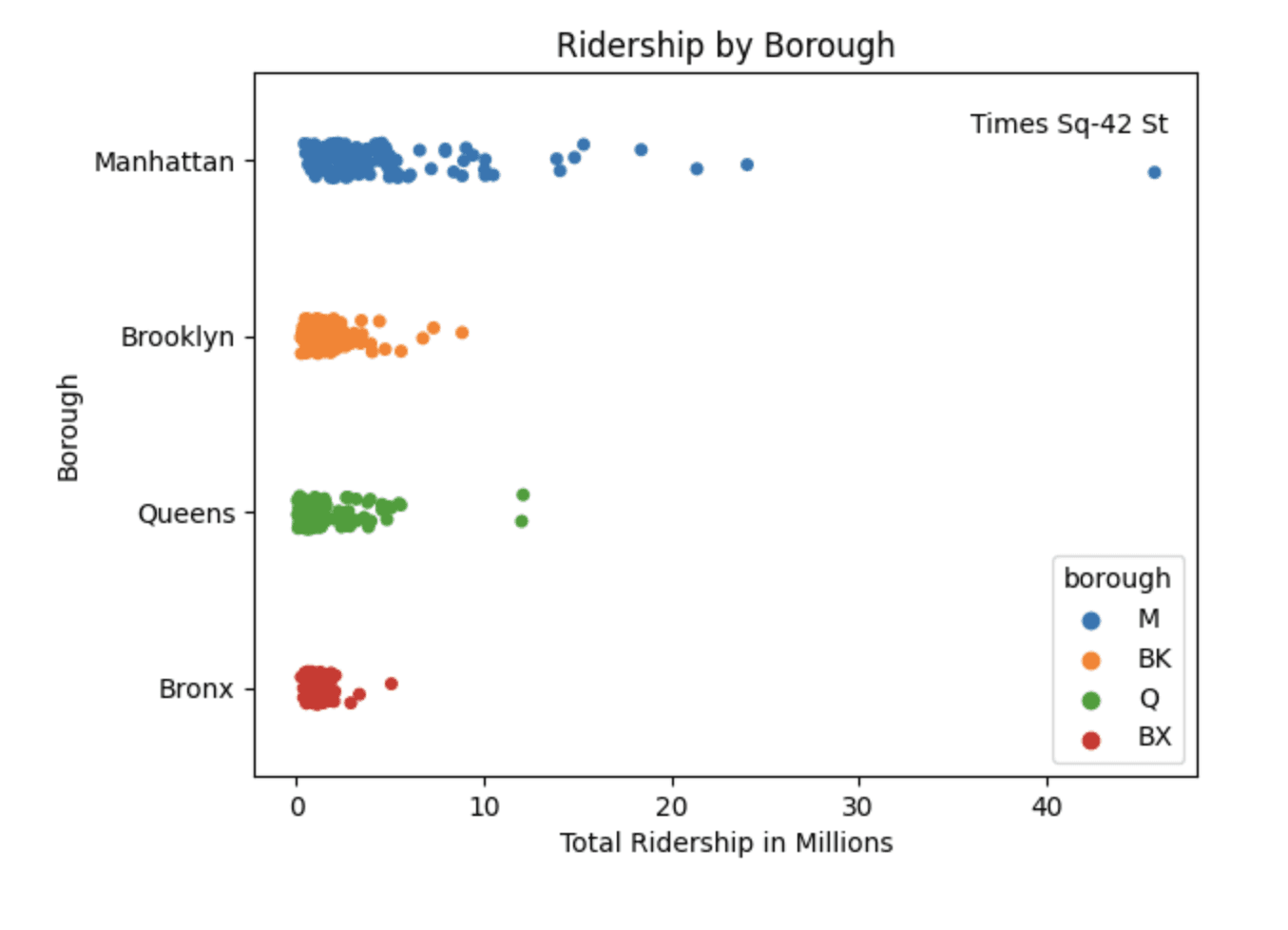

Ridership by day of the week

# make a new column called day_of_week using the transit_timestamp column
df['day_of_week'] = df['transit_timestamp'].dt.day_name()

# Extract the date part from the datetime values and assign to a new column
df.loc[:, 'date_only'] = df['transit_timestamp'].dt.date

# Get the count of unique calendar days
unique_days_count = df['date_only'].nunique()

# Display the result
print("Count of unique calendar days:", unique_days_count)

Count of unique calendar days: 365

Group dataframe by day_of_week

by_day = df.groupby(['day_of_week'])['ridership'].sum().reset_index()

by_day.shape

Reorder the dates by setting up a list of days

lst = ["Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday","Sunday"]
by_day["day_of_week"] = pd.Categorical(by_day["day_of_week"], categories=lst, ordered=True)

# Sort the DataFrame based on the custom order of the 'day_of_week' column
by_day = by_day.sort_values("day_of_week")

# Reset the index if needed
by_day = by_day.reset_index(drop=True)

Get the average ridership per day

by_day['ridership_per_day'] = by_day['ridership'] / 365

Make a plot using ridership_per_day

# plot the ridership_per_day
by_day['ridership_per_day'].plot(kind='bar')
plt.title('Number of Riders by Day of the Week')
plt.xlabel('Day of the Week')
plt.ylabel('Number of Daily Riders')
plt.xticks(rotation=45)
plt.xticks(range(7), lst, rotation=65)
plt.show()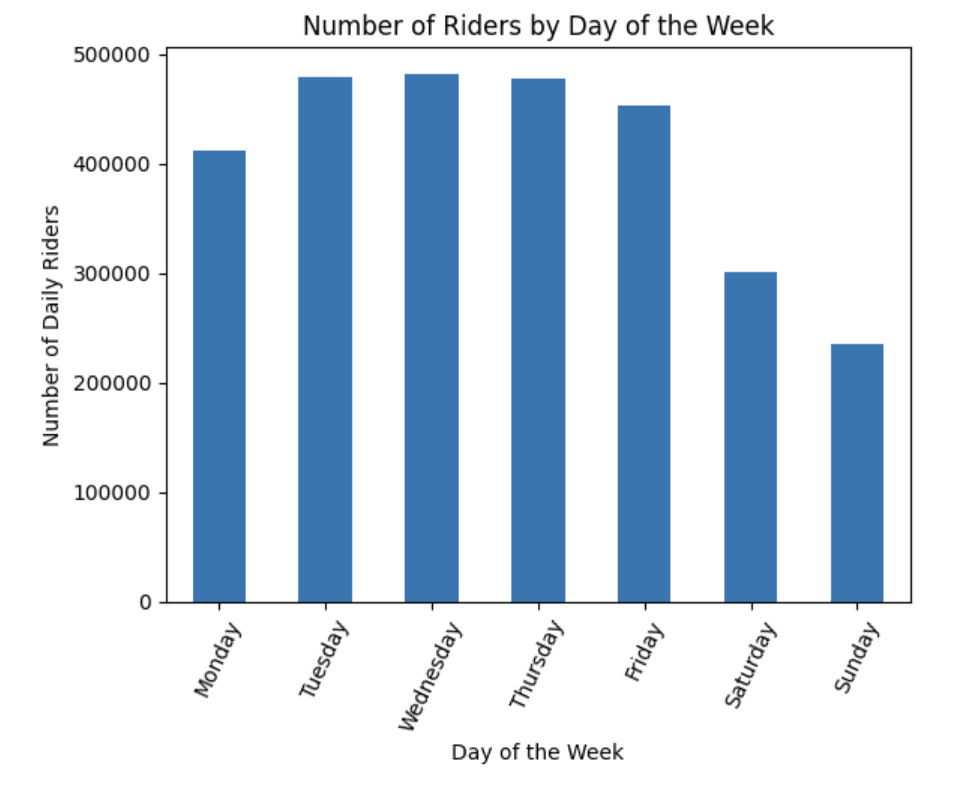

We can see that the middle of the work week tends to have the highest number of riders, with a significant decrease on the weekends. We can create a similar visualization to see the ridership by month.

Find and plot the ridership by month

df.loc[:, 'month_only'] = df['transit_timestamp'].dt.month

by_month = df.groupby(['month_only'])['ridership'].sum().reset_index()
by_month['ridership_per_month'] = (by_month['ridership'] / 12).round().astype(int)
by_month.head()

plt.bar(by_month['month_only'], by_month['ridership_per_month'])
plt.xlabel('Month')
plt.ylabel('Ridership')
plt.title('Ridership per Month')
plt.xticks(by_month['month_only'], ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct','Nov', 'Dec'])
plt.show()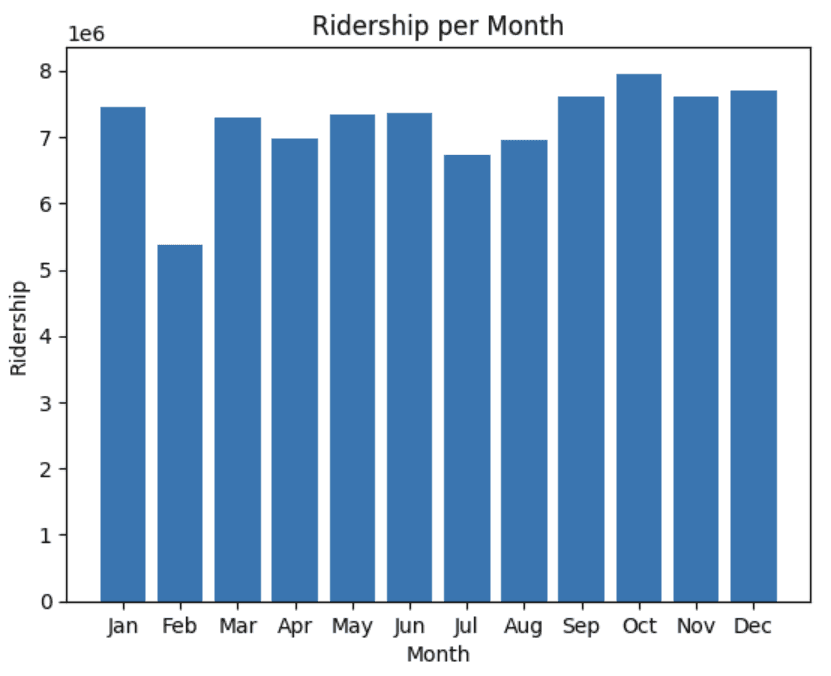

We see a large decrease in February and a slight drop off during July and August. This is likely due to February only having 28 days and July and August being the summer months which would correlate with vacation frequency.

Number of Riders by hour

# Extract the hour from 'transit_timestamp'
df['hour'] = df['transit_timestamp'].dt.hour

# Calculate the average number of riders for each hour
average_riders_per_hour = df.groupby('hour')['ridership'].mean()

# Plot the data
plt.figure(figsize=(10, 6))
plt.plot(average_riders_per_hour.index, average_riders_per_hour.values, marker='o', linestyle='-')
plt.xlabel('Hour of the Day')
plt.ylabel('Average Number of Riders')
plt.title('Average Number of Riders per Hour')
plt.xticks(average_riders_per_hour.index)
plt.grid(True)
plt.show()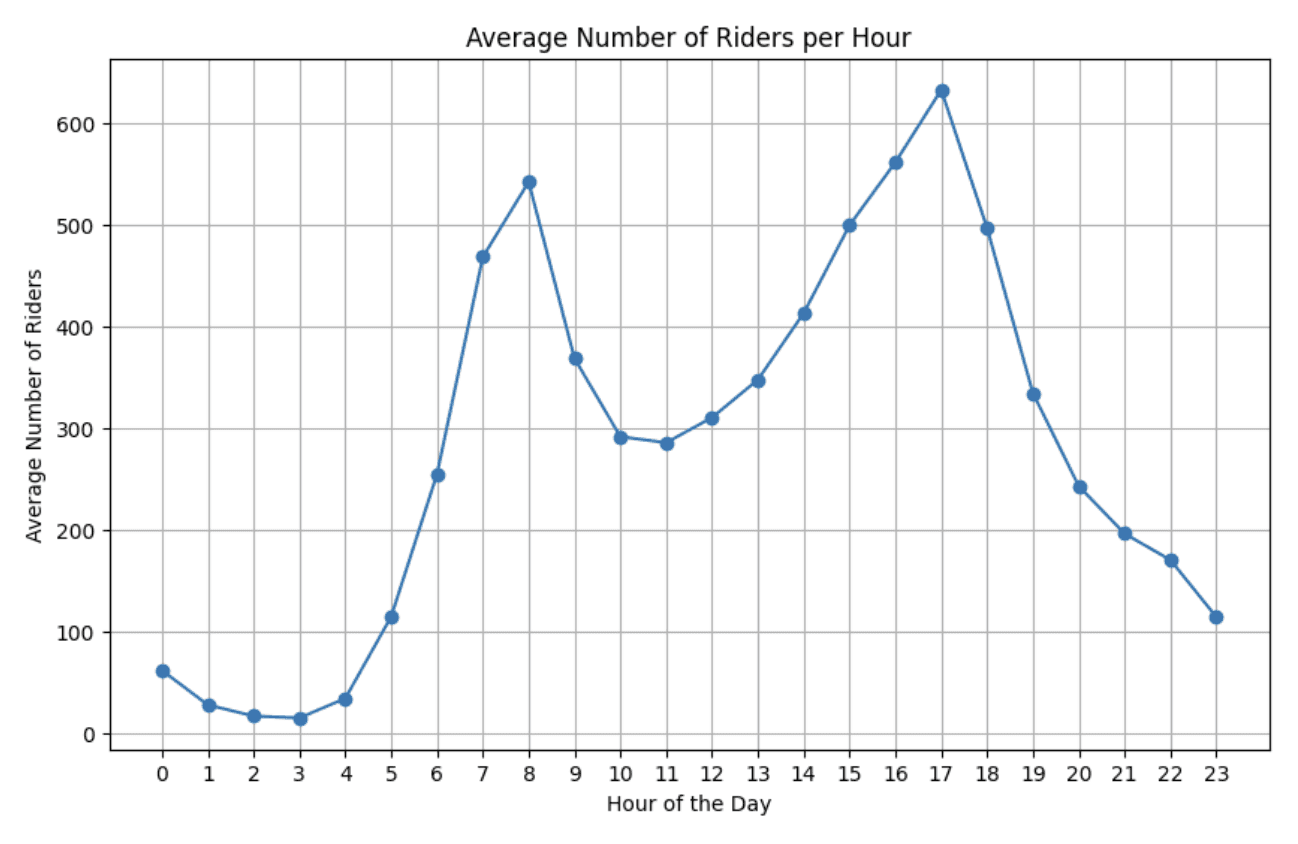

Most Popular Stations

Popularity based by average ridership

top_10_stations = by_station_df.sort_values(by=['ridership'], ascending=False).head(10)

# Borough colors
borough_colors = {'M': 'blue', 'BK': 'orange', 'Q': 'green', 'BX': 'red'}

plt.figure(figsize=(10, 5))

# Plot each bar separately with the specified color
for i, station in enumerate(top_10_stations['station_complex']):
    plt.barh(station, top_10_stations['ridership'].iloc[i], color=borough_colors[top_10_stations['borough'].iloc[i]])

plt.title('Top 10 Stations with Highest Traffic', fontsize=20)
plt.xlabel('Ridership', fontsize=15)
plt.ylabel('Station', fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.gca().invert_yaxis()

# Create custom legend for borough colors
handles = [plt.Rectangle((0, 0), 1, 1, color=borough_colors[borough]) for borough in borough_colors]
labels = list(borough_colors.keys())
plt.legend(handles, labels, title='Borough')

plt.show()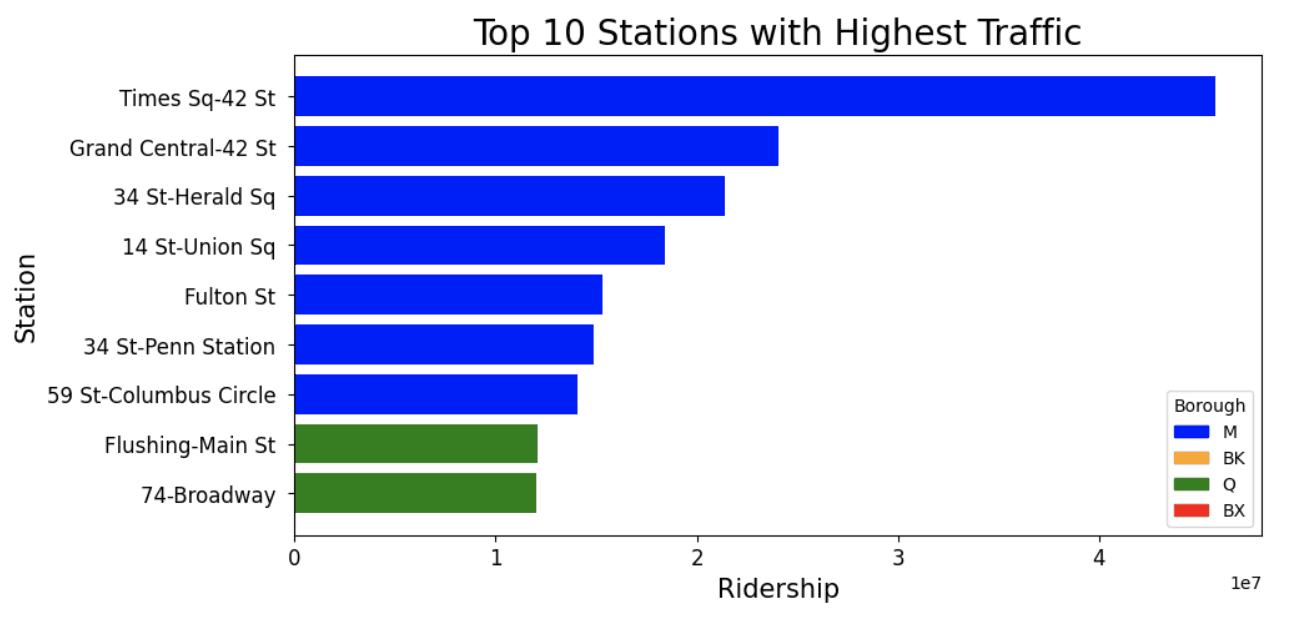

How much usage do the top 10 stations account for?

# sum of all ridership in by_station_df
total_ridership = by_station_df['ridership'].sum()
top_10_ridership = top_10_stations['ridership'].sum()

percentage_of_ridership_from_top10 = top_10_ridership / total_ridership * 100
print(f"Percentage of total ridership from the 10 most popular stations: {percentage_of_ridership_from_top10:.2f}%")

# get total number of rows in the dataframe
stations_total = len(by_station_df)
print(f"These 10 stations only account for {((10/stations_total)*100):.2f}% of the total number of stations")

Percentage of total ridership from the 10 most popular stations: 18.51% These 10 stations only account for 2.36% of the total number of stations

4. Predicting Ridership

If we can create a model to predict ridership at any given time, this would be an incredibly useful tool for the MTA to use. This would allow them to better plan for maintenance, staffing, and other resources. This data set is limited to only a few factors that could affect ridership, but it is a good starting point and will indicate if it is possible to create a model to predict ridership.

I chose to use Random Forest Regression for this task because we needed to choose a model that can handle non-linear data and it is not prone to overfitting.

# make a new dataframe called rfr_df
rfr_df = pd.DataFrame()

Prep the new data frame

rfr_df['month'] = original_df['transit_timestamp'].dt.month
rfr_df['day'] = original_df['transit_timestamp'].dt.day
rfr_df['hour'] = original_df['transit_timestamp'].dt.hour
rfr_df['ridership'] = original_df['ridership']

rfr_df = rfr_df.groupby(['month', 'day', 'hour'])['ridership'].sum().reset_index()

rfr_df.head()

Decide key features and split your data into testing and training.

X = rfr_df[['month', 'day', 'hour']]
y = rfr_df['ridership']

# Split the data into 80% training and 20% testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Instantiate RFR model, train and make predictions…

# Split the data into features and labels
labels = np.array(rfr_df['ridership'])
features = rfr_df.drop('ridership', axis=1)
feature_list = list(features.columns)
features = np.array(features)

# Split the data into training and testing sets
train_features, test_features, train_labels, test_labels = train_test_split(
    features, labels, test_size=0.25, random_state=38
)

# Instantiate model with decision trees
rf = RandomForestRegressor(n_estimators=400, random_state=38)

# Train the model on training data
rf.fit(train_features, train_labels)

# Make predictions on the test set
predictions = rf.predict(test_features)

# Calculate the absolute errors
errors = abs(predictions - test_labels)

# Print out the mean absolute error (MAE)
mae = mean_absolute_error(test_labels, predictions)
print('Mean Absolute Error:', round(mae, 2), 'riders.')

# Calculate the R-squared (R2)
r2 = r2_score(test_labels, predictions)
print('R-squared (R2):', round(r2, 2))

# Calculate and display Mean Absolute Percentage Error (MAPE) and Accuracy
mape = 100 * (errors / test_labels)
accuracy = 100 - np.mean(mape)
print('Accuracy:', round(accuracy, 2), '%.')

# Create a scatter plot to visualize the predictions vs. actual values
plt.figure(figsize=(10, 6))
plt.scatter(test_labels, predictions, alpha=0.7)
plt.plot([min(test_labels), max(test_labels)], [min(test_labels), max(test_labels)], 'r--')

plt.xlabel('Actual Ridership')
plt.ylabel('Predicted Ridership')
plt.title('Random Forest Regressor: Actual vs. Predicted Ridership')
plt.show()

Mean Absolute Error: 31931.12 riders.

R-squared (R2): 0.88

Accuracy: 75.47 %.

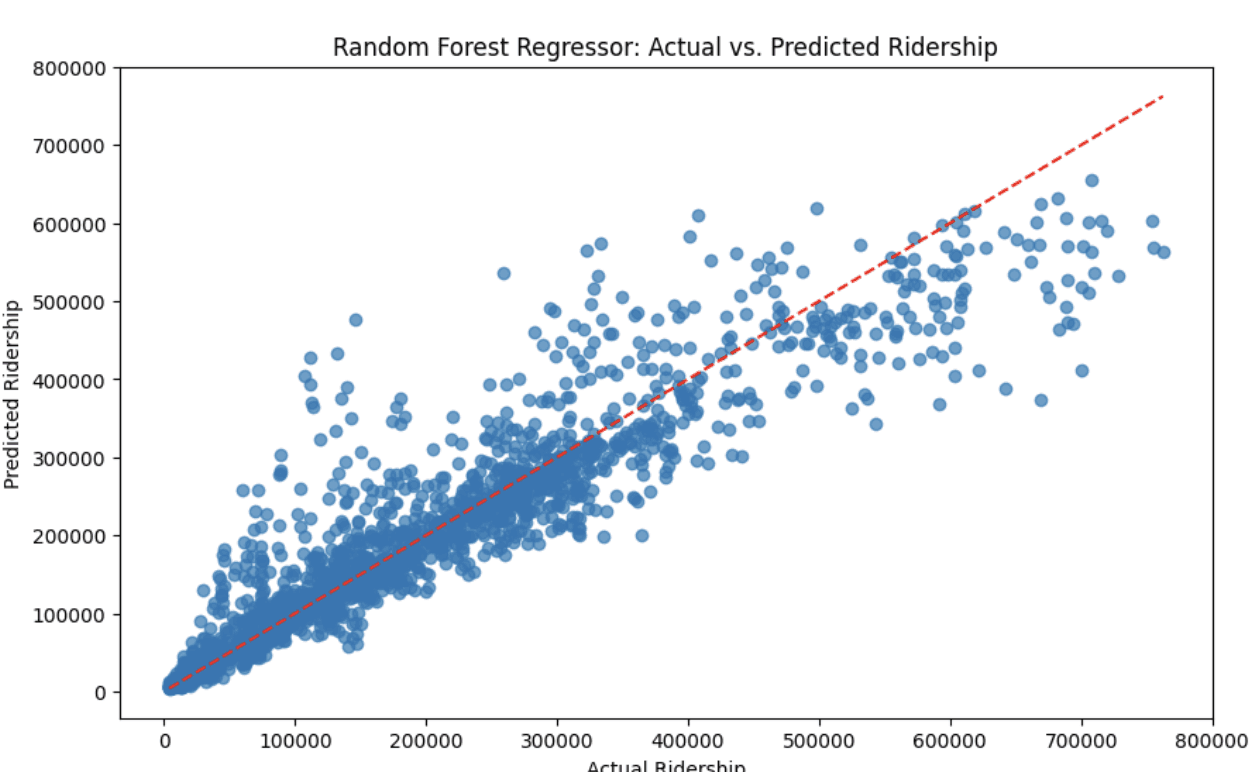
We can see we got an impressive R2 score of 0.88. This indicates that our model has potential to fit the data. This was only based on three factors. Unfortunately, the model has a mean absolute error of around 32 thousand. However if more factors were added to the model, it could potentially be improved, such as weather, unique stations, holidays, etc.

What are the most important features in our model?

# Train the model on training data
rf.fit(train_features, train_labels)

# Get feature importances
feature_importances = rf.feature_importances_

# Associate feature importances with feature names
feature_importance_list = list(zip(feature_list, feature_importances))

# Print the top N most important features and their importances
for feature, importance in feature_importance_list:
    print(f"{feature}: {importance}")

# Create a bar plot to visualize feature importances
plt.figure(figsize=(10, 6))
plt.bar(range(len(feature_importances)), feature_importances)
plt.xticks(range(len(feature_importances)), [feature[0] for feature in feature_importance_list], rotation='vertical')
plt.xlabel('Features')
plt.ylabel('Importance')
plt.title('Feature Importances')
plt.show()

month: 0.25222014283065824

day: 0.13287063052608278

hour: 0.6149092266432591

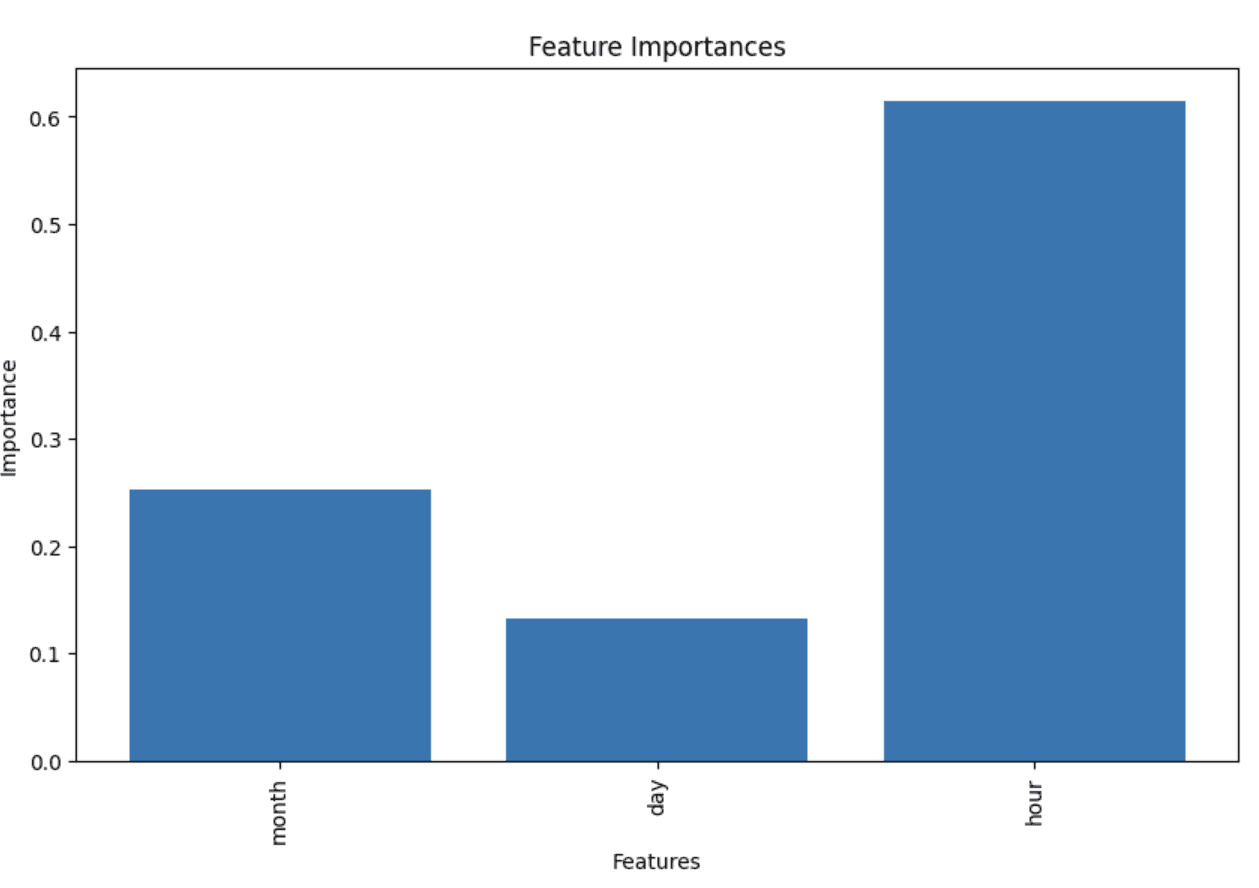
The hour of day is a major indicator on the amount of ridership.

Function for predicting ridership

def predict_and_show_ridership(month, day, hour):
    input_data = np.array([[month, day, hour]])
    predicted_ridership = rf.predict(input_data)
    actual_ridership = rfr_df[(rfr_df['month'] == month) & (rfr_df['day'] == day) & (rfr_df['hour'] == hour)]['ridership'].values[0]
    
    print(f"Input: Month={month}, Day={day}, Hour={hour}")
    print(f"Predicted Ridership: {round(predicted_ridership[0], 2)}")
    print(f"Actual Ridership: {actual_ridership}")

Test the function

# Test the function with a specific input
predict_and_show_ridership(month=5, day=5, hour=12)

Input: Month=5, Day=5, Hour=12

Predicted Ridership: 286930.37

Actual Ridership: 299513

predict_and_show_ridership(month=3, day=27, hour=2)

Input: Month=3, Day=27, Hour=2

Predicted Ridership: 15467.66

Actual Ridership: 15270

Conclusion

This analysis has successfully shown that many of the potential goals of the analysis can be answered using data

Schedule maintenance and improve crowd management
This analysis shows we can easily determine the trends for which stations, time of day and day of the week have the most riders. This information can be used to schedule maintenance and improve crowd management. We did this through bar charts, strip plots, and tree maps.

Ridership by location
It is also clear that by using geovisualization and exploratory data analysis techniques, we can see which boroughs and stations have the most riders. The heat map and dash app are great tools to visualize this data. The heat map and further information about visualizing the data can be found here.

Predicting Ridership
We were able to predict ridership with a high degree of accuracy. This shows that there is potential to build a model to predict ridership. I believe that given the right data, this model could be improved and reliably predict how many riders will be at a given station at a given time.

Understanding the dataset

Potential Goals of Analysis

What is the best time to schedule maintenance?
Which factors are most important to ridership (time of day, day of week, etc.)?
Which part of the city has the most riders? Which Borough?
Which station sees the most riders?
Does Subway usage have seasonal trends?
Is there potential to build a model to predict ridership?

Overall by answering these questions and gaining a further understanding of ridership, it should highlight that the MTA could use data to improve crowd management, service performance and maintenance scheduling.

The most necessary columns for our analysis are the following:

transit_timestamp (to identify the time of day)
station_complex (to identify the station)
ridership (to identify the number of people entering the station at a given time)
latitude / longitude / Georeference (to identify the location of the station)

1. Importing the required libraries

import pandas as pd # for data manipulation and analysis
import numpy as np

import seaborn as sns # for data visualization
import matplotlib.pyplot as plt
import plotly.express as px

import dash # for building interactive visualizations
from dash import dcc, html, Input, Output

import geopandas as gpd # for geographic data manipulation
from shapely.geometry import Point, Polygon

from sklearn.model_selection import train_test_split # for machine learning
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score

2. Preparing the data

Read CSV to Dataframe

# read csv file to pd dataframe
df = pd.read_csv('MTA_Subway_Hourly_Ridership__Beginning_February_2022.csv')

Preparing the data for datetime format

# change transit_timestamp to datetime object
df['transit_timestamp'] = pd.to_datetime(df['transit_timestamp'])

Make a copy before slicing the dataset

original_df = df.copy()

Get data for one year

# Filter data for the specified time range
start_date = pd.Timestamp('2022-02-01')
end_date = pd.Timestamp('2023-02-01')
df = df[(df.transit_timestamp >= start_date) & (df.transit_timestamp < end_date)]

# check the earliest and latest time of the data
print(df['transit_timestamp'].min())
print(df['transit_timestamp'].max())

Output:

2022-02-01 00:00:00 2023-01-31 23:00:00

Clean the names of the stations by removing the route numbers

# remove the () and everything in between the () from each station_complex row in the df
df['station_complex'] = df['station_complex'].str.replace(r'\(.*\)', '', regex=True)

Preparing the data for geovisualization

# make geodataframe out of df
gdf = gpd.GeoDataFrame(df, geometry=gpd.points_from_xy(df['longitude'], df['latitude']))

geo_stations_df = gdf.groupby(['station_complex_id', 'station_complex', 'borough', 'latitude','longitude', 'geometry'])['ridership'].sum().reset_index()

3. Exploratory Data Analysis

How many subway stations in our dataset?

# print the number of unique station complex ids
print(df['station_complex_id'].nunique())

423

Create a new dataframe grouped by station and ridership

by_station_df = df.groupby(['station_complex_id', 'station_complex', 'borough', 'latitude', 'longitude'])['ridership'].sum().reset_index() by_station_df.shape

Riders by borough

## get the total ridership by borough
boroughs = df.groupby('borough')['ridership'].sum()
boroughs

borough
BK 237932586
BX 81994749
M 560176396
Q 156471936

Visualizing the amount of ridership by borough

fig = px.treemap(boroughs, path=[boroughs.index], values=boroughs.values, title='Subway Ridership by Borough')
fig.show()

We can see that Manhattan has the most ridership, followed by Brooklyn, Queens and the Bronx.

Visualizing the number of stations by borough

station_count = by_station_df['borough'].value_counts()
borough_names = ['Brooklyn', 'Manhattan', 'Queens', 'Bronx']

fig = px.bar(x = borough_names, y = station_count.values, 
       color = station_count.index, text = station_count.values, 
       title = 'Number of Stations by Borough')

fig.update_layout( xaxis_title = "Boroughs", yaxis_title = "Subway Stations")
fig.show()

We can see that Manhattan actually has less stations despite having the most ridership.

# make a copy of by_station_df and divide the ridership by 1 Million to normalize the data to millions
by_station_df_normalize = by_station_df.copy()
by_station_df_normalize['ridership'] = by_station_df_normalize['ridership']/1000000

sns.stripplot(x=by_station_df_normalize['ridership'], y=by_station_df_normalize['borough'], hue=by_station_df_normalize['borough'])
plt.yticks([0, 1, 2, 3], ['Manhattan', 'Brooklyn', 'Queens', 'Bronx']) 
plt.xlabel('Total Ridership in Millions')
plt.ylabel('Borough')
plt.annotate('Times Sq-42 St', xy=(0.76, 0.915), xycoords='axes fraction')
plt.title('Ridership by Borough')
plt.show()

Ridership by day of the week

# make a new column called day_of_week using the transit_timestamp column
df['day_of_week'] = df['transit_timestamp'].dt.day_name()

# Extract the date part from the datetime values and assign to a new column
df.loc[:, 'date_only'] = df['transit_timestamp'].dt.date

# Get the count of unique calendar days
unique_days_count = df['date_only'].nunique()

# Display the result
print("Count of unique calendar days:", unique_days_count)

Count of unique calendar days: 365

Group dataframe by day_of_week

by_day = df.groupby(['day_of_week'])['ridership'].sum().reset_index()

by_day.shape

Reorder the dates by setting up a list of days

lst = ["Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday","Sunday"]
by_day["day_of_week"] = pd.Categorical(by_day["day_of_week"], categories=lst, ordered=True)

# Sort the DataFrame based on the custom order of the 'day_of_week' column
by_day = by_day.sort_values("day_of_week")

# Reset the index if needed
by_day = by_day.reset_index(drop=True)

Get the average ridership per day

by_day['ridership_per_day'] = by_day['ridership'] / 365

Make a plot using ridership_per_day

# plot the ridership_per_day
by_day['ridership_per_day'].plot(kind='bar')
plt.title('Number of Riders by Day of the Week')
plt.xlabel('Day of the Week')
plt.ylabel('Number of Daily Riders')
plt.xticks(rotation=45)
plt.xticks(range(7), lst, rotation=65)
plt.show()

Find and plot the ridership by month

df.loc[:, 'month_only'] = df['transit_timestamp'].dt.month

by_month = df.groupby(['month_only'])['ridership'].sum().reset_index()
by_month['ridership_per_month'] = (by_month['ridership'] / 12).round().astype(int)
by_month.head()

plt.bar(by_month['month_only'], by_month['ridership_per_month'])
plt.xlabel('Month')
plt.ylabel('Ridership')
plt.title('Ridership per Month')
plt.xticks(by_month['month_only'], ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct','Nov', 'Dec'])
plt.show()

Number of Riders by hour

# Extract the hour from 'transit_timestamp'
df['hour'] = df['transit_timestamp'].dt.hour

# Calculate the average number of riders for each hour
average_riders_per_hour = df.groupby('hour')['ridership'].mean()

# Plot the data
plt.figure(figsize=(10, 6))
plt.plot(average_riders_per_hour.index, average_riders_per_hour.values, marker='o', linestyle='-')
plt.xlabel('Hour of the Day')
plt.ylabel('Average Number of Riders')
plt.title('Average Number of Riders per Hour')
plt.xticks(average_riders_per_hour.index)
plt.grid(True)
plt.show()

Most Popular Stations

Popularity based by average ridership

top_10_stations = by_station_df.sort_values(by=['ridership'], ascending=False).head(10)

# Borough colors
borough_colors = {'M': 'blue', 'BK': 'orange', 'Q': 'green', 'BX': 'red'}

plt.figure(figsize=(10, 5))

# Plot each bar separately with the specified color
for i, station in enumerate(top_10_stations['station_complex']):
    plt.barh(station, top_10_stations['ridership'].iloc[i], color=borough_colors[top_10_stations['borough'].iloc[i]])

plt.title('Top 10 Stations with Highest Traffic', fontsize=20)
plt.xlabel('Ridership', fontsize=15)
plt.ylabel('Station', fontsize=15)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.gca().invert_yaxis()

# Create custom legend for borough colors
handles = [plt.Rectangle((0, 0), 1, 1, color=borough_colors[borough]) for borough in borough_colors]
labels = list(borough_colors.keys())
plt.legend(handles, labels, title='Borough')

plt.show()

How much usage do the top 10 stations account for?

# sum of all ridership in by_station_df
total_ridership = by_station_df['ridership'].sum()
top_10_ridership = top_10_stations['ridership'].sum()

percentage_of_ridership_from_top10 = top_10_ridership / total_ridership * 100
print(f"Percentage of total ridership from the 10 most popular stations: {percentage_of_ridership_from_top10:.2f}%")

# get total number of rows in the dataframe
stations_total = len(by_station_df)
print(f"These 10 stations only account for {((10/stations_total)*100):.2f}% of the total number of stations")

Percentage of total ridership from the 10 most popular stations: 18.51% These 10 stations only account for 2.36% of the total number of stations

4. Predicting Ridership

I chose to use Random Forest Regression for this task because we needed to choose a model that can handle non-linear data and it is not prone to overfitting.

# make a new dataframe called rfr_df
rfr_df = pd.DataFrame()

Prep the new data frame

rfr_df['month'] = original_df['transit_timestamp'].dt.month
rfr_df['day'] = original_df['transit_timestamp'].dt.day
rfr_df['hour'] = original_df['transit_timestamp'].dt.hour
rfr_df['ridership'] = original_df['ridership']

rfr_df = rfr_df.groupby(['month', 'day', 'hour'])['ridership'].sum().reset_index()

rfr_df.head()

Decide key features and split your data into testing and training.

X = rfr_df[['month', 'day', 'hour']]
y = rfr_df['ridership']

# Split the data into 80% training and 20% testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Instantiate RFR model, train and make predictions…

# Split the data into features and labels
labels = np.array(rfr_df['ridership'])
features = rfr_df.drop('ridership', axis=1)
feature_list = list(features.columns)
features = np.array(features)

# Split the data into training and testing sets
train_features, test_features, train_labels, test_labels = train_test_split(
    features, labels, test_size=0.25, random_state=38
)

# Instantiate model with decision trees
rf = RandomForestRegressor(n_estimators=400, random_state=38)

# Train the model on training data
rf.fit(train_features, train_labels)

# Make predictions on the test set
predictions = rf.predict(test_features)

# Calculate the absolute errors
errors = abs(predictions - test_labels)

# Print out the mean absolute error (MAE)
mae = mean_absolute_error(test_labels, predictions)
print('Mean Absolute Error:', round(mae, 2), 'riders.')

# Calculate the R-squared (R2)
r2 = r2_score(test_labels, predictions)
print('R-squared (R2):', round(r2, 2))

# Calculate and display Mean Absolute Percentage Error (MAPE) and Accuracy
mape = 100 * (errors / test_labels)
accuracy = 100 - np.mean(mape)
print('Accuracy:', round(accuracy, 2), '%.')

# Create a scatter plot to visualize the predictions vs. actual values
plt.figure(figsize=(10, 6))
plt.scatter(test_labels, predictions, alpha=0.7)
plt.plot([min(test_labels), max(test_labels)], [min(test_labels), max(test_labels)], 'r--')

plt.xlabel('Actual Ridership')
plt.ylabel('Predicted Ridership')
plt.title('Random Forest Regressor: Actual vs. Predicted Ridership')
plt.show()

Mean Absolute Error: 31931.12 riders.

R-squared (R2): 0.88

Accuracy: 75.47 %.

What are the most important features in our model?

# Train the model on training data
rf.fit(train_features, train_labels)

# Get feature importances
feature_importances = rf.feature_importances_

# Associate feature importances with feature names
feature_importance_list = list(zip(feature_list, feature_importances))

# Print the top N most important features and their importances
for feature, importance in feature_importance_list:
    print(f"{feature}: {importance}")

# Create a bar plot to visualize feature importances
plt.figure(figsize=(10, 6))
plt.bar(range(len(feature_importances)), feature_importances)
plt.xticks(range(len(feature_importances)), [feature[0] for feature in feature_importance_list], rotation='vertical')
plt.xlabel('Features')
plt.ylabel('Importance')
plt.title('Feature Importances')
plt.show()

month: 0.25222014283065824

day: 0.13287063052608278

hour: 0.6149092266432591

The hour of day is a major indicator on the amount of ridership.

Function for predicting ridership

def predict_and_show_ridership(month, day, hour):
    input_data = np.array([[month, day, hour]])
    predicted_ridership = rf.predict(input_data)
    actual_ridership = rfr_df[(rfr_df['month'] == month) & (rfr_df['day'] == day) & (rfr_df['hour'] == hour)]['ridership'].values[0]
    
    print(f"Input: Month={month}, Day={day}, Hour={hour}")
    print(f"Predicted Ridership: {round(predicted_ridership[0], 2)}")
    print(f"Actual Ridership: {actual_ridership}")

Test the function

# Test the function with a specific input
predict_and_show_ridership(month=5, day=5, hour=12)

Input: Month=5, Day=5, Hour=12

Predicted Ridership: 286930.37

Actual Ridership: 299513

predict_and_show_ridership(month=3, day=27, hour=2)

Input: Month=3, Day=27, Hour=2

Predicted Ridership: 15467.66

Actual Ridership: 15270

Conclusion

This analysis has successfully shown that many of the potential goals of the analysis can be answered using data

More projects

Design

2023

MoMA Data Visualization

More projects

Design

2023

MoMA Data Visualization

Home

Projects

Stack

Contact

Resume

nick gentz (1)

Understanding the dataset

Potential Goals of Analysis

Overall by answering these questions and gaining a further understanding of ridership, it should highlight that the MTA could use data to improve crowd management, service performance and maintenance scheduling.

1. Importing the required libraries

2. Preparing the data

Read CSV to Dataframe

Preparing the data for datetime format

Get data for one year

Clean the names of the stations by removing the route numbers

Preparing the data for geovisualization

3. Exploratory Data Analysis

Riders by borough

Visualizing the number of stations by borough

Ridership by day of the week

Find and plot the ridership by month

Number of Riders by hour

Most Popular Stations

4. Predicting Ridership

Function for predicting ridership

Conclusion

This analysis has successfully shown that many of the potential goals of the analysis can be answered using data

Understanding the dataset

Potential Goals of Analysis

Overall by answering these questions and gaining a further understanding of ridership, it should highlight that the MTA could use data to improve crowd management, service performance and maintenance scheduling.

1. Importing the required libraries

2. Preparing the data

Read CSV to Dataframe

Preparing the data for datetime format

Get data for one year

Clean the names of the stations by removing the route numbers

Preparing the data for geovisualization

3. Exploratory Data Analysis

Riders by borough

Visualizing the number of stations by borough

Ridership by day of the week

Find and plot the ridership by month

Number of Riders by hour

Most Popular Stations

4. Predicting Ridership

Function for predicting ridership

Conclusion

This analysis has successfully shown that many of the potential goals of the analysis can be answered using data

More projects

MoMA Data Visualization

More projects

MoMA Data Visualization